2 Metodologia
A pesquisa busca compreender a forma como a arguição de descumprimento de preceito fundamental é operacionalizada no campo do processo no Supremo Tribunal Federal a fim de judicializar a política. Trata-se de um estudo empírico, observando o método indutivo e de abordagem quali-quantitativa. Ademais, a pesquisa apoia-se em ferramentas computacionais.
O estudo será dividido em três momentos. No primeiro realizar-se-á uma revisão narrativa de literatura brasileira sobre a judicialização da política, suas dimensões e intersecções com a literatura não-brasileira. Para tanto, selecionou-se as teses, dissertações e artigos indexados no Portal Brasileiro de Publicações e Dados Científicos em Acesso Aberto (Oasisbr) com os descritores “judicialização da política”, “arguição de descumprimento de preceito fundamental”, “constitucionalismo democrático” e “diálogos institucionais”. Foram selecionados os registros publicados nos últimos 5 anos e com pertinência temática com esta pesquisa.
No segundo momento será realizada a coleta, manipulação e tratamento dos dados referentes às arguições de descumprimento de preceito fundamental ajuizadas entre 2014 e 2024. A organização dos dados possibilita a visualização do objeto de pesquisa e sua categorização. Por fim, os dados em texto coletados, manipulados e tratados serão analisados por meio da análise de conteúdo a fim de inferir a operacionalização das arguições para o fenômeno da judicialização da política.
A pesquisa, portanto, não segue uma metodologia única, mas aproveita de diferentes instrumentos e técnicas para a consecução dos seus objetivos. A triangulação metodológica permite a observação do objeto de estudo em sua complexidade. O multimétodo, segundo Simone Tuzzo e Claudomilson Braga (2016), é
uma forma de integrar diferentes perspectivas no fenômeno em estudo, como forma de descoberta de paradoxos e contradições, ou como forma de desenvolvimento no sentido de utilizar sequencialmente os métodos para que o recurso ao método inicial informe a utilização do segundo método […]. Des[t]e modo a possibilidade da triangulação mesmo em se tratando da mesma perspectiva – qualitativa – parece ser uma abordagem que se sustenta e faz sentido à medida que oferece ao pesquisador olhares múltiplos e diferentes do mesmo lugar de fala (Tuzzo; Braga, 2016, p. 155–156).
Dessa forma, o multimétodo produzirá “tipos diferentes de dados e resultam em formas diferentes de conhecimento” sem que necessariamente uma técnica seja utilizada para confirmar a outra (Oliveira, 2015, p. 139). O que se busca é um processo consecutivo de aplicação das metodologias que resultarão, ao final, na solução do problema geral sem ignorar a complexidade do objeto de estudo (Paranhos et al., 2016).
A análise de dados permitirá a observação quantitativa do objeto de pesquisa, além de que a inferência sobre os seus resultados fornecerá subsídios preliminares à análise de conteúdo. Nesse sentido, “exploratory data analysis can never be the whole story, but nothing else can serve as the foundation stone – as the first step” (Tukey, 1977, p. 3).
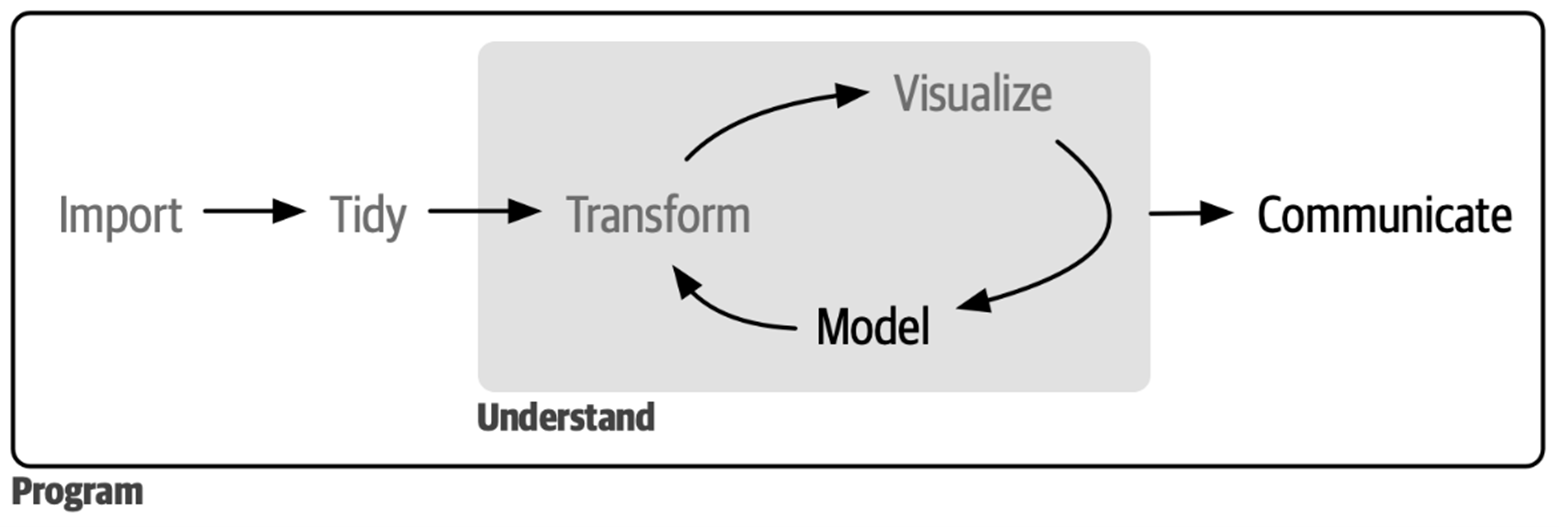
A análise exploratória dos dados (AED) é, portanto, o primeiro processo da análise de dados e não possui um procedimento rígido pré-estabelecido, mas fornece ao pesquisador um espaço para busca de ideias. Trata-se de uma etapa preliminar que busca compreender os dados e necessita da criatividade do pesquisador (Wickham; Çetinkaya-Rundel; Grolemund, 2023).
No geral, o processo de análise de dados pode ser resumido na Figura 2.1 abaixo:
Um levantamento no portal de jurisprudências do Supremo Tribunal Federal na época da escrita do projeto de dissertação em 2023, buscando por decisões em ADPF retornou 485 acórdãos e 1.250 decisões monocráticas (sem aplicar recorte temporal). Trabalhar com corpus extensos manualmente limitaria a pesquisa pois seria necessário realizar muitos recortes sobre os documentos para que fosse viabilizada. Nesse sentido, os avanços computacionais permitiram a automatização das técnicas de análise de conteúdo (Izumi; Moreira, 2018).
Segundo Maurício Izumi e Davi Moreira (2018, p. 40),
o uso do texto como dado para análise automatizada de conteúdo permite: (1) a utilização de diferentes técnicas independentemente do idioma sob análise; (2) o cálculo de medidas de incerteza, sendo possível julgar se as diferenças entre os textos são substantivas ou apenas fruto de erros de mensuração e variação amostral; (3) reduzir a necessidade de intervenção humana, facilitando a replicabilidade dos resultados; (4) a análise de um volume de informações manualmente inviável.
Não obstante, a automatização da análise de conteúdo atua no processamento do texto e não substitui a análise do pesquisador, mas “make possible inferences that were previously impossible” (Grimmer; Stewart, 2013, p. 495).
O processamento automatizado dos textos permite, portanto, substituir parte das etapas da análise de conteúdo. O texto será processado pelo software e analisado pelo pesquisador. Diferentes funções computacionais podem gerar codificações que, após a leitura do corpus, permitirá a categorização e análise.
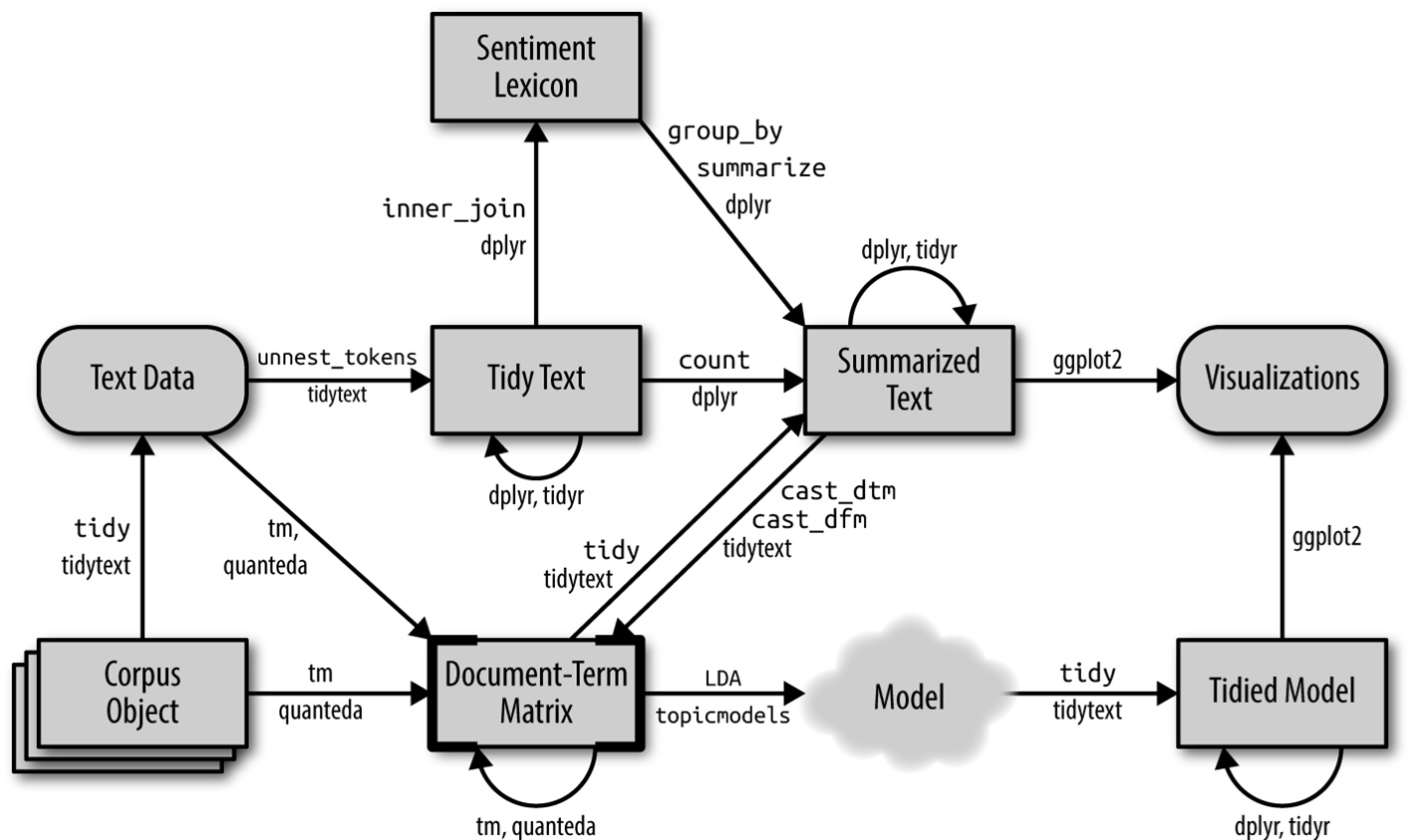
Como referência metodológica, o artigo de Maurício Izumi e Davi Moreira apresenta diferentes modelos de trabalho do texto como dado (Izumi; Moreira, 2018) e organiza nas seguintes etapas: 1) obtenção dos dados; 2) pré-processamento dos dados; e o processamento dos dados. O pré-processamento compreende diversas etapas de preparação do texto para o trabalho no software. O processamento dos dados será escolhido após a visualização do corpus. A Figura 2.2 abaixo ilustra o processo de trabalhar com texto como dado:
As analises criadas pelo pesquisador serão intersecionais com os resultados produzidos pelo Interface de R pour les Analyses Multidimensionnelles de Textes et de Questionnaires (IRaMuTeQ), especialmente da aplicação do Método de Reinert – classificação hierárquica descendente (Reinert, 1990).
Com essas análises, pretende-se verificar como o Tribunal e seus ministros respondem aos partidos políticos que judicializam a política, analisando o conteúdo dos diferentes instrumentos de decisão. O conjunto de métodos aplicados permite a observação da judicialização da política na sua multidimensionalidade.
Sobre a perspectiva macrometodológica desta pesquisa, pode-se situá-la no campo da jurimetria. Como expõe José Mário Neto, Luis Felipe Barbosa e Alexandre Moura Filho (2022, p. 19), “as pesquisas no campo jurídico devem ir além da dogmática, mediante a utilização de pesquisas efetivamente empíricas, a partir do levantamento, da compreensão e do tratamento dos dados nos diferentes contextos jurídicos trabalhados”.
Embora as metodologias tradicionais da pesquisa jurídica sejam insubstituíveis na compreensão do “dever ser”, elas se mostram insuficientes para capturar a complexidade do “ser” do direito, ou seja, suas aplicações, dinâmicas institucionais e impactos. Nesse sentido, a opção pela jurimetria não representa uma ruptura ou negação da tradição jurídica, mas sim uma expansão de seu arsenal metodológico. O objetivo é construir uma ponte entre a teoria e a prática, utilizando dados para testar hipóteses, identificar padrões e, em última instância, informar uma análise qualitativa mais robusta e contextualizada, permitindo assim uma compreensão mais complexa do direito (Siqueira; Moreira; Vieira, 2023).
A jurimetria, enquanto disciplina, pode ser formalmente definida como a aplicação de métodos estatísticos e quantitativos ao estudo do Direito, abrindo um caminho para investigar o funcionamento da ordem jurídica, identificar padrões de julgamento e, com isso, conferir maior previsibilidade e cientificidade ao Direito (Loevinger, 1949).
A pertinência da abordagem jurimétrica se acentua sobremaneira quando observamos as características do sistema jurídico brasileiro contemporâneo. A consolidação de um sistema de precedentes vinculantes conclama os tribunais a manterem sua jurisprudência estável, íntegra e coerente, torna a análise sistemática e quantitativa dos julgados não apenas uma ferramenta útil, mas uma necessidade metodológica para aferir a eficácia de tal sistema. Ademais, em um cenário de crescente debate público sobre o ativismo judicial e a judicialização da política, fenômenos que colocam o STF no centro de controvérsias de grande repercussão nacional, a jurimetria emerge como um poderoso instrumento de transparência e accountability (Siqueira; Moreira; Vieira, 2023).
Ela permite que a academia e a sociedade civil analisem objetivamente as decisões da mais alta corte, deslocando a discussão do campo das impressões anedóticas e das narrativas passionais para o terreno das conclusões fundamentadas em evidências empíricas. Em vez de simplesmente aplaudir ou criticar o “ativismo”, a metodologia jurimétrica possibilita mapear quando, como, em que temas e em favor de quais atores o tribunal exerce seu poder por meio de instrumentos como a ADPF (Siqueira; Moreira; Vieira, 2023). Portanto, a jurimetria não se apresenta apenas como um método de pesquisa, mas como uma ferramenta de controle social sobre o Poder Judiciário, capaz de avaliar a eficácia de suas decisões e fomentar um debate público mais qualificado sobre seu papel institucional na democracia brasileira.
Em síntese, o delineamento metodológico desta dissertação articula o rigor da análise de dados com a profundidade da interpretação jurídica para investigar o fenômeno da judicialização da política nas ADPF. A abordagem jurimétrica, longe de se apresentar como uma panaceia, é proposta como uma ferramenta estratégica para superar as limitações de uma análise puramente dogmática, permitindo a construção de uma base de evidências empíricas sobre o comportamento do STF. Ao mapear sistematicamente os atores, os temas e os resultados, a pesquisa oferece subsídios para um debate mais informado, objetivo e menos especulativo sobre o papel do STF na democracia brasileira.
A contribuição esperada é, portanto, dupla. Do ponto de vista substantivo, busca-se produzir um conhecimento sobre como a judicialização da política se manifesta concretamente no âmbito das ADPF. Do ponto de vista metodológico, a dissertação almeja servir como um estudo de caso sobre como a jurimetria pode ser aplicada de forma transparente, rigorosa e relevante na pesquisa acadêmica em Direito, demonstrando seu valor para transformar discussões constitucionais centrais de um campo de batalha de opiniões para um terreno de análise científica, fortalecendo assim a credibilidade e o impacto da produção de conhecimento na área jurídica.
2.1 Análise de sobrevivência: Estimador Kaplan-Meier
A mensuração do tempo no processo judicial constitui um desafio metodológico fundamental para a compreensão da efetividade da prestação jurisdicional. No âmbito do STF, onde as Arguições de Descumprimento de Preceito Fundamental representam um instrumento de elevado impacto político e social, a análise da sua duração é um indicador da capacidade de resposta da Corte a questões constitucionais. Contudo, as abordagens tradicionais para medir essa duração, como o cálculo da média ou da mediana do tempo de tramitação, revelam-se inadequadas e enganosas. Essas métricas, embora intuitivas, padecem de uma falha estrutural: só podem ser calculadas para os processos que já alcançaram um desfecho, ou seja, que foram “baixados”. Ao desconsiderarem sistematicamente os processos que ainda se encontram em tramitação no momento da coleta de dados, essas abordagens introduzem um viés de subestimação. Os casos que são resolvidos mais rapidamente são sobrerrepresentados na amostra, enquanto os processos mais longos e complexos, que permanecem ativos, são completamente ignorados. O resultado é uma fotografia distorcida da realidade, que pode levar a conclusões equivocadas sobre a celeridade do Tribunal, mascarando a existência de um passivo de casos de longa duração.
A consequência direta desse viés metodológico é a produção de um conhecimento incompleto sobre o funcionamento do tribunal. O estudo que se propõe a analisar a duração das ADPFs ajuizadas entre 2013 e 2023, com a coleta de dados encerrada ao final de 2024. Ao calcular o tempo médio de tramitação, o pesquisador incluiria apenas as ações que foram iniciadas e concluídas nesse intervalo. Uma ADPF ajuizada em 2015 e que ainda aguarda julgamento em 2024 seria excluída da análise. O tempo médio resultante seria, portanto, artificialmente reduzido, pois se basearia exclusivamente no subconjunto de processos “rápidos”. Essa limitação não é trivial; ela compromete a validade externa de qualquer inferência sobre a eficiência judicial. Para superar essa barreira, é preciso adotar um arcabouço metodológico que não apenas tolere, mas que seja especificamente desenhado para incorporar a informação contida nos casos ainda pendentes.
Para superar as deficiências das métricas tradicionais, esta pesquisa adota inicialmente a análise de sobrevivência. Originalmente desenvolvida em campos como a medicina, para estudar o tempo até o óbito de pacientes, e a engenharia, para analisar o tempo até a falha de componentes mecânicos, esta técnica estatística tem se mostrado versátil e poderosa para a análise de fenômenos em diversas áreas, incluindo as ciências sociais e, mais recentemente, o direito. A sua aplicação em estudos sobre o sistema de justiça permite investigar com rigor a duração de processos judiciais, carreiras de magistrados ou o tempo até a reincidência criminal (Fukumoto; Masuyama, 2015; Mine et al., 2025). O cerne da análise de sobrevivência é o estudo do “tempo-até-o-evento” (time-to-event), que, no contexto desta dissertação, se traduz no tempo decorrido desde a autuação de uma ADPF no STF até a ocorrência do “evento de interesse” - definido como a “baixa do processo”. Esta abordagem promove uma mudança de paradigma fundamental na pergunta de pesquisa: em vez de questionar “qual a duração média de uma ADPF?”, passamos a investigar “qual a probabilidade de uma ADPF ‘sobreviver’ (isto é, permanecer ativa e sem decisão final) para além de um determinado ponto no tempo?”.
O pilar que sustenta a superioridade da análise de sobrevivência em estudos longitudinais é o seu tratamento rigoroso do fenômeno da “censura” (censoring). Em termos estatísticos, a censura ocorre quando o tempo exato até o evento de interesse não é conhecido para um ou mais sujeitos da amostra, embora se tenha informação parcial sobre ele (Lesko et al., 2018; Prinja; Gupta; Verma, 2010). No contexto desta dissertação, uma ADPF que foi autuada e que permanece “em tramitação” na data final de coleta de dados é um exemplo observação censurada. Não se sabe quando ela será concluída, mas se sabe, com certeza, que o seu tempo de “sobrevivência” é, no mínimo, igual ao período entre sua autuação e o fim do estudo.
O conceito de censura, longe de ser um mero artifício estatístico, está intrinsecamente ligado à realidade da litigância no Supremo Tribunal Federal. A forma predominante de censura nesta pesquisa é a “censura administrativa”, que ocorre quando o próprio desenho do estudo impõe uma data de corte para a observação. Nesta dissertação, todos os processos que não forem baixados até a data final de coleta de dados serão administrativamente censurados.
Tendo estabelecido a análise de sobrevivência como ponto de partida metodológico e a censura como seu conceito-chave, a ferramenta específica escolhida para iniciar a operacionalização desta abordagem é o estimador de Kaplan-Meier, também conhecido como “estimador do limite do produto” (product-limit estimator) (Borgan, 2005).
Sua principal característica e maior vantagem, sobretudo para a análise de fenômenos sociais complexos como a atividade judicial, é sua natureza não-paramétrica - isso significa que o método não exige quaisquer pressuposições sobre a forma da distribuição estatística dos tempos de duração dos processos (Borgan, 2005; Lins; Figueiredo; Rocha, 2017). Em outras palavras, não é necessário assumir que os tempos de tramitação seguem uma curva pré-definida, como a distribuição normal ou exponencial. O estimador de Kaplan-Meier permite que os próprios dados, com suas idiossincrasias e irregularidades, ditem a forma da curva de sobrevivência.
Para compreender como o estimador de Kaplan-Meier opera na prática, é essencial analisar sua formulação matemática. A fórmula do estimador de Kaplan-Meier para a função de sobrevivência no tempo \(t\), denotada por \(\hat{S}(t)\), é expressa da seguinte forma:
\[ \hat{S}(t) = \prod_{t_i \leq t} {\Bigg(1 - \frac{d_i}{n_i} \Bigg)} \]
Onde \(d_i\) é o número de eventos de interesse que ocorreram no tempo \(t_i\) e \(n_i\) é o número de indivíduo em risco de sofrer o evento imediatamente antes do tempo \(t_i\).
Esta expressão calcula a sobrevivência cumulativa através da multiplicação de uma série de probabilidades condicionais de sobrevivência. O cálculo é refeito em cada ponto no tempo \(t_i\), onde ocorre pelo menos um evento. \(\hat{S}(t)\) é a função de sobrevivência estimada, ou seja, qual a estimativa de sobrevivência de um indivíduo no tempo \(t\).
A razão \(\frac{d_i}{n_i}\) indica a probabilidade condicional de falha. Trata-se de uma probabilidade condicional pois não indica a probabilidade geral de um processo ser baixado, mas sim a probabilidade de ser baixado no tempo \(t_i\) considerando que sobreviveu até aquele ponto. A probabilidade condicional de falha é subtraída de 1, fornecendo a probabilidade condicional de sobrevivência \(\Big(1 - \frac{d_i}{n_i}\Big)\). Em outras palavras, se a probabilidade condicional de falha era 0,15, a probabilidade condicional de sobrevivência é de 1 - 0,15 ou 0,85.
Por fim, deve-se considerar que para que um processo “sobreviva” até um tempo distante, digamos 36 meses, ele precisa necessariamente ter sobrevivido a todos os intervalos de tempo anteriores. A lógica é cumulativa: a probabilidade de sobreviver até o mês 36 é o produto da probabilidade de sobreviver ao mês 1, multiplicada pela probabilidade de, tendo sobrevivido ao mês 1, sobreviver também ao mês 2, e assim por diante, até o mês 36. O estimador de Kaplan-Meier aplica essa lógica calculando a probabilidade de sobrevivência apenas nos momentos discretos em que um evento realmente ocorre. Assim, o produtório instrui o cálculo a multiplicar todas as probabilidades condicionais de sobrevivência.
Essa abordagem em cadeia, baseada na lei da multiplicação de probabilidades para eventos sucessivos, é o que permite ao estimador construir a curva de sobrevivência passo a passo, refletindo a diminuição gradual da probabilidade de um processo permanecer ativo à medida que o tempo avança.
Contudo, é fundamental reconhecer a principal limitação do estimador de Kaplan-Meier: ele é uma ferramenta essencialmente descritiva e univariada. Ele pode descrever com precisão a curva de sobrevivência de um grupo de processos e permitir a comparação entre as curvas de diferentes grupos (por exemplo, ADPFs de diferentes relatores) através de testes como o log-rank. No entanto, o método não consegue, por si só, determinar quais fatores ou variáveis influenciam a duração do processo, nem quantificar o impacto de cada um. Ele nos diz “o quê” e “quando”, mas não “por quê”. Para responder a perguntas como “O perfil do ministro relator afeta o tempo de tramitação?” ou “Processos com rito abreviado são julgados mais rapidamente, controlando por outros fatores?”, é necessário recorrer a outros modelos.
Esta limitação, no entanto, não diminui o valor do Estimador de Kaplan-Meier; ao contrário, posiciona-o como o primeiro passo essencial em uma análise de sobrevivência, fornecendo a descrição do fenômeno sobre a qual modelos mais complexos, como o Modelo de Riscos Proporcionais de Cox, podem ser construídos para explorar as relações causais.
2.2 Análise de sobrevivência: modelo de riscos proporcionais de Cox
O estimador de Kaplan-Meier, detalhado na seção anterior, é uma ferramenta descritiva de valor inestimável. Ele nos permite visualizar e quantificar a probabilidade de um processo permanecer ativo ao longo do tempo, tratando adequadamente os dados censurados e fornecendo uma imagem fidedigna da dinâmica temporal da baixa processual. Contudo, sua principal limitação reside em sua natureza univariada. A curva de Kaplan-Meier pode nos dizer se existe uma diferença na “sobrevivência” processual entre dois, mas ela não consegue explicar as razões por trás dessa diferença, nem isolar o efeito de uma variável específica enquanto controla o impacto de outras. É para preencher essa lacuna analítica que esta dissertação emprega o Modelo de Riscos Proporcionais de Cox, também conhecido como Regressão de Cox.
Para entender como o modelo funciona, é preciso primeiro compreender seu conceito central: a função de risco, também chamada de hazard function ou taxa de falha instantânea, denotada por \(h(t)\). A função de risco, no contexto desta pesquisa, pode ser entendida como o “potencial instantâneo” ou o “risco iminente” de um processo ser baixado no exato instante de tempo \(t\), dado que ele “sobreviveu” (permaneceu ativo) até aquele momento. É uma medida da propensão à baixa em um ponto específico no tempo. Enquanto a função de sobrevivência de Kaplan-Meier nos diz a probabilidade de um processo ainda estar ativo após um tempo \(t\), a função de risco nos informa a intensidade com que a “força da baixa” atua sobre os processos que ainda estão na fila de julgamento naquele instante.
O Modelo de Cox, então, não modela diretamente o tempo de sobrevivência, mas sim como a função de risco de um processo é afetada por suas características específicas. A distinção do modelo reside em sua capacidade de separar a função de risco em duas partes distintas. A primeira é a função de risco de base (baseline hazard) \(h_0 (t)\), que representa o risco de baixa ao longo do tempo para um processo “de referência” hipotético, cujas características são todas nulas ou estão em um nível de base. A segunda parte descreve como o risco de base é modificado (multiplicado) pelas características (covariáveis) de cada processo individual. Essa estrutura permite isolar e quantificar o efeito de cada variável sobre o risco de baixa, respondendo a perguntas como: “A presença de um relator aumenta ou diminui o risco de um processo ser baixado, e em que magnitude?”.
O pilar sobre o qual todo o Modelo de Cox se assenta é a premissa dos riscos proporcionais (proportional hazards assumption). Esta premissa estabelece que o efeito de uma variável preditora (covariável) sobre a função de risco é multiplicativo e constante ao longo do tempo. Em termos mais simples, isso significa que a razão entre as taxas de risco de dois indivíduos (ou dois processos) com características diferentes permanece constante durante todo o período de observação.
A fórmula expressa como a taxa de risco instantânea para um determinado processo, em um tempo \(t\), depende de suas características (covariáveis). Para um processo com um conjunto de \(p\) covariáveis \((X_1,X_2,…,X_p )\), a função de risco \(h(t,X)\) é dada por:
\[ h(t,X)=h_0 (t)×exp(β_1 X_1+β_2 X_2+⋯+β_p X_p ) \] Esta equação estabelece que o risco de um processo ser concluído em um determinado tempo \(t\), dada as suas características específicas \(X\), é o produto do risco base e um fator multiplicador.
A função de risco base \(h_0 (t)\) (baseline hazard function) representa o risco de o evento ocorrer no tempo \(t\) para um processo hipotético cujas covariáveis são iguais a zero. O multiplicador de risco \(exp(β_1 X_1+β_2 X_2+⋯+β_p X_p )\) age sobre a função de risco base. O multiplicador de risco é composto pela combinação linear das covariáveis e dos respectivos coeficientes.
As covariáveis são as variáveis independentes da nossa pesquisa, ou seja, os fatores que hipotetizamos influenciar a duração do processo. Em nossa análise das ADPFs, exemplos de covariáveis incluem o tipo de autor, a existência de um pedido de medida cautelar ou o rito. Este termo, portanto, quantifica como o conjunto de características de um processo específico modifica o risco base, escalando-o para cima (se o efeito combinado das covariáveis for de aceleração) ou para baixo (se o efeito for de retardamento).
Os termos \(β_1,β_2,…,β_p\) são os coeficientes de regressão, cada um está associado a uma covariável e mede a magnitude e a direção do efeito daquela variável sobre a função de risco. Uma vez que a interpretação do logaritmo não é intuitiva, foca-se no sinal do coeficiente: um coeficiente \(β\) positivo indica que um aumento na variável \(X\) está associado a um aumento no risco, o que se traduz em um tempo de tramitação mais curto (o processo é acelerado). Inversamente, um coeficiente \(β\) negativo indica que um aumento na variável \(X\) está associado a uma diminuição no risco, implicando um tempo de tramitação mais longo (o processo é retardado).
Embora o modelo de Cox estime os coeficientes \(β\), a sua interpretação direta como efeito no logaritmo do risco é pouco intuitiva. Por essa razão, o padrão é transformar esses coeficientes em uma medida de efeito mais acessível: a Razão de Riscos, ou Hazard Ratio (HR). O HR é calculado simplesmente pela exponenciação do coeficiente \(β\), ou seja, \(HR=exp(β)\). O HR quantifica o efeito de uma covariável de forma multiplicativa e relativa. Ele informa em que proporção o risco de ocorrência do evento muda para cada aumento de uma unidade na covariável, mantendo todas as outras constantes.
Um HR maior que 1 indica que a covariável aumenta o risco, associando-se a um tempo de tramitação mais curto (aceleração). Por exemplo, um HR de 1.8 significa que o risco de conclusão é 80% maior para o grupo com aquela característica. Um HR menor que 1 indica que a covariável diminui o risco, associando-se a um tempo de tramitação mais longo (retardamento). Por exemplo, um HR de 0.7 significa que o risco de conclusão é 30% menor. Finalmente, um HR igual a 1 indica que a covariável não tem qualquer efeito sobre o risco de conclusão do processo.
A adoção do Modelo de Regressão de Cox representa um avanço metodológico para a análise da duração processual. Sua principal vantagem é a capacidade de estimar o efeito de múltiplas covariáveis (sejam elas binárias, categóricas ou contínuas) sobre o tempo até o evento, controlando por seus efeitos simultâneos e lidando de forma robusta com dados censurados. No entanto, o modelo não é isento de limitações. Sua validade depende criticamente da premissa de riscos proporcionais. Se o efeito de uma variável muda ao longo do tempo, o modelo padrão pode produzir estimativas enviesadas. Todavia, o modelo permite, ao fim, testar hipóteses derivadas da teoria do direito e da ciência política, quantificando a importância relativa de diferentes variáveis e contribuindo para um diagnóstico mais preciso sobre os gargalos e os aceleradores da prestação jurisdicional.
2.3 Análise de Correspondência (AC)
A Análise de Correspondência (AC) surge como a ferramenta metodológica para realizar uma “cartografia jurídica” do campo das ADPFs. Diferentemente de técnicas estatísticas que buscam estabelecer relações de causalidade linear, a AC é uma técnica exploratória e multidimensional cuja vocação primordial é a visualização da estrutura de associações em um conjunto de dados categóricos (Silva, 2012). O objetivo da AC é transformar uma complexa tabela de dados - que cruza, por exemplo, os proponentes das ADPFs com os resultados dos julgamentos - em um mapa perceptual de fácil interpretação. Nesse mapa, as afinidades, oposições e distâncias entre as diferentes categorias revelam a estrutura oculta do campo, permitindo identificar quais atores se associam a quais desfechos e quais são os eixos de oposição fundamentais que organizam o espaço decisório do STF. Desta forma, a AC nos permite ir além da análise caso a caso para desvelar a gramática sistêmica que rege a judicialização da política na mais alta corte do país.
A AC trata de uma técnica eminentemente exploratória e descritiva, e não confirmatória ou inferencial. Seu propósito não é testar uma hipótese causal pré-definida (como, por exemplo, “o legitimado X causa o resultado Y”), mas sim explorar um conjunto de dados complexos para revelar padrões, tendências e estruturas de associação que não são imediatamente visíveis. Em outras palavras, a AC funciona como um microscópio ou telescópio para o cientista social, permitindo-lhe simplificar a complexidade dos dados e gerar hipóteses fundamentadas sobre as relações entre as variáveis. Esta distinção é necessária, pois orienta a interpretação dos resultados: o mapa gerado pela AC não oferece provas de causalidade, mas sim uma representação visual e estruturada das correspondências existentes no universo analisado, que por sua vez demanda interpretação teórica e análise qualitativa para ser plenamente compreendida (Sarah, 2025).
A técnica parte de uma tabela de contingência, que nada mais é do que uma tabela de dupla entrada que cruza as frequências de duas ou mais variáveis categóricas, e a converte em um gráfico bidimensional, comumente chamado de “mapa perceptual” ou “biplot”. Neste mapa, cada categoria das variáveis analisadas é representada por um ponto. A distinção do método reside nesta transposição do numérico para o espacial, pois permite que o pesquisador utilize sua capacidade intuitiva de interpretar distâncias e posições para apreender a estrutura dos dados de forma quase instantânea. Em vez de se perder em uma miríade de números e percentagens, o pesquisador pode, com um único olhar, identificar os principais agrupamentos, as oposições mais marcantes e as categorias que se destacam no conjunto (Bortoli; Birck, 2017; Sarah, 2025; Silva, 2012).
Para mensurar a associação entre as categorias, a AC parte de um conceito basilar: a hipótese de independência estatística. Antes de podermos dizer que duas categorias estão associadas, precisamos de um ponto de referência, um cenário de “não associação” contra o qual comparar a realidade. Este cenário é o da independência, uma situação hipotética na qual as variáveis de linha e de coluna não teriam qualquer relação entre si. No contexto desta pesquisa, a independência significaria que o tipo de proponente de uma ADPF não teria absolutamente nenhuma influência sobre o resultado do julgamento. Nesse mundo hipotético, a proporção de decisões “Procedentes”, “Improcedentes” etc., seria exatamente a mesma para todos os tipos de proponentes (partidos políticos, governadores, entidades de classe) e seria igual à proporção geral de cada resultado no total de ADPFs analisadas.
Com base nesse referencial de independência, podemos definir os dois elementos centrais para o cálculo da associação: as frequências observadas e as frequências esperadas. As frequências observadas (\(f_o\)) são os dados empíricos, os números reais que constam em tabela de contingência. Representam, por exemplo, o número de vezes que, de fato, uma ADPF proposta por um partido político foi julgada procedente. São o retrato da realidade que coletamos. Em contrapartida, as frequências esperadas (\(f_e\)) são as frequências teóricas que nós esperaríamos encontrar em cada célula da tabela se a hipótese de independência fosse verdadeira. O cálculo da frequência esperada para cada célula é simples: multiplica-se o total da linha correspondente pelo total da coluna correspondente e divide-se pelo total geral de observações. A comparação entre o que foi observado (\(f_o\)) e o que seria esperado em um cenário de ausência de relação (\(f_e\)) é o cerne da análise.
A Análise de Correspondência utiliza essa comparação para construir uma métrica geométrica: a distância qui-quadrado (\(\chi^2\)). Enquanto em outros contextos o teste qui-quadrado é usado apenas para obter um valor de significância estatística, na AC ele é a base para definir a própria geometria do espaço que se quer mapear. A distância qui-quadrado mede, para cada célula, o quão longe a frequência observada está da frequência esperada, levando em conta o tamanho relativo da célula. A lógica é que quanto maior a discrepância entre o observado e o esperado, mais forte é a “atração” ou “repulsão” entre a categoria da linha e a categoria da coluna em questão, e maior será essa distância. A soma de todas essas distâncias individuais compõe a variabilidade total do sistema. É essa métrica de distância que permite posicionar os pontos (as categorias) em um mapa, de forma que a distância visual entre eles seja uma representação fiel da sua dissimilaridade estatística. O mapa perceptual, portanto, não é uma mera ilustração, mas uma projeção geométrica rigorosa das relações de associação contidas na tabela de dados original.
A principal virtude da AC reside em sua capacidade de realizar uma “redução de dimensionalidade”. Uma tabela de contingência, mesmo que com poucas linhas e colunas, representa um espaço multidimensional complexo. O objetivo da AC é decompor a inércia total em menos dimensões ortogonais (ou seja, independentes entre si), chamadas de eixos principais. O método identifica, matematicamente, um primeiro eixo que, sozinho, consegue explicar a maior porcentagem possível da inércia total. Este eixo representa a oposição mais fundamental, a clivagem mais importante que estrutura os dados. Em seguida, ele encontra um segundo eixo, perpendicular ao primeiro, que explica a maior parte da inércia restante, e assim sucessivamente. O objetivo prático é conseguir representar a maior parte da informação original (idealmente, acima de 80%) utilizando apenas os dois ou três primeiros eixos, o que permite a criação de um mapa bidimensional sem uma perda significativa de informação.
A inércia pode ser conceitualmente entendida como a quantidade total de “variância” ou “informação” contida na tabela de contingência. É uma medida que quantifica o grau em que os dados se afastam da hipótese de independência. Se as frequências observadas fossem idênticas às esperadas, a inércia seria zero, indicando ausência total de estrutura ou associação. Quanto maior o valor da inércia, mais estruturado é o conjunto de dados e mais fortes são as associações entre as categorias de linha e coluna. Ela quantifica o quanto o sistema decisório do STF, como um todo, se desvia de um modelo de neutralidade perfeita em relação à identidade dos proponentes.
Em síntese, a adoção da AC nesta dissertação se justifica por sua capacidade de oferecer uma visão de conjunto, estrutural e relacional, sobre um fenômeno multifacetado. Ao invés de se limitar a uma análise sequencial e fragmentada dos casos, a AC permite visualizar a totalidade do campo decisório, revelando as afinidades eletivas entre tipos de atores e tipos de resultados, bem como as clivagens fundamentais que organizam este espaço. A técnica funciona como uma ferramenta exploratória, capaz de gerar hipóteses empiricamente fundamentadas sobre a lógica de funcionamento da Corte, que podem então ser aprofundadas por meio da análise qualitativa.
Contudo, a honestidade intelectual e o rigor metodológico exigem o reconhecimento explícito das limitações desta abordagem. A principal limitação da AC é que ela revela associações, e não causalidade. A proximidade entre “Partido Político” e “Procedente” no mapa não nos autoriza a concluir que ser um partido causa a vitória; apenas indica que essas duas categorias aparecem juntas com uma frequência significativamente maior do que o esperado pelo acaso. Ademais, é importante lembrar que o mapa perceptual é um modelo, uma representação simplificada da realidade, e não a realidade em si. As escolhas de categorização e a redução de dimensionalidade implicam necessariamente em alguma perda de informação.
2.4 Classificação Hierárquica Descendente (CHD)
A análise de conteúdo, como sistematizada por Laurence Bardin (1995), representa um pilar metodológico nas ciências sociais e jurídicas para a interpretação de textos e documentos. Tradicionalmente, a pesquisa em Direito se vale de abordagens hermenêuticas e qualitativas para a exegese de leis, doutrinas e decisões judiciais. Contudo, o cenário contemporâneo impõe um desafio de escala sem precedentes. Instituições como o STF produzem um volume colossal de dados textuais, tornando a análise manual de todo um corpo jurisprudencial sobre um tema específico uma tarefa hercúlea, senão impraticável. Diante dessa realidade, a pesquisa jurídica é compelida a buscar novas ferramentas que permitam lidar com grandes volumes de informação sem sacrificar o rigor analítico. É nesse contexto que emerge a lexicometria, uma abordagem que emprega a estatística para a análise de dados textuais, operacionalizada por softwares como o IRaMuTeQ (Interface de R pour les Analyses Multidimensionnelles de Textes et de Questionnaires). Este método não substitui a interpretação qualitativa, mas a potencializa, oferecendo um caminho para identificar padrões, estruturas latentes e tendências discursivas em vastos corpora documentais. A adoção de tal metodologia, portanto, não é uma mera preferência por inovação, mas uma adaptação necessária à “dataficação” do universo jurídico.
Para investigar os textos as decisões do STF, esta dissertação adota como técnica central a Classificação Hierárquica Descendente (CHD), também conhecida como Método de Reinert. Esta abordagem transcende a simples contagem de frequência de palavras, objetivando a identificação de “mundos lexicais” - definidos como universos semânticos estáveis, caracterizados pela coocorrência sistemática de um determinado vocabulário dentro de um corpus. A premissa fundamental do método é que a organização do vocabulário em um texto não é aleatória; pelo contrário, padrões distintos de uso de palavras correspondem a diferentes estruturas de pensamento, quadros de referência ou, no contexto jurídico, a distintas lógicas argumentativas e posições enunciativas (Marpsat, 2010; Reinert, 1990).
A CHD, ao agrupar segmentos de texto com vocabulário similar, permite ao pesquisador mapear esses mundos lexicais e, consequentemente, desvelar a estrutura temática subjacente ao discurso analisado. Sua aplicação às decisões do STF permite desconstruir a aparente unidade monolítica de um acórdão ou de um voto, revelando como diferentes lógicas são mobilizadas, por vezes em tensão, dentro do mesmo universo discursivo.
O nome Classificação Hierárquica Descendente encapsula a lógica operacional do método. “Classificação” refere-se ao seu objetivo principal: agrupar unidades textuais (segmentos de texto) com base na semelhança de seu vocabulário. “Hierárquica” indica que os grupos resultantes, denominados classes, são organizados em uma estrutura aninhada, similar a uma árvore genealógica, que é visualmente representada por um dendrograma. Finalmente, “Descendente” (ou divisiva) descreve o processo algorítmico: a análise parte do corpus inteiro como um único bloco e o divide sucessivamente em subgrupos menores, mais específicos e com maior coesão interna. O objetivo final é gerar um conjunto de classes que sejam, simultaneamente, o mais homogêneas possível em seu interior (o vocabulário dentro de uma classe está fortemente associado) e o mais heterogêneas possível em relação às demais (o vocabulário de uma classe é estatisticamente distinto do vocabulário das outras).
O primeiro passo prático e conceitualmente importante da CHD é a preparação e segmentação do corpus. Após a compilação dos textos integrais das decisões das ADPFs em um único arquivo, o software realiza a partição do texto em “Segmentos de Texto” (ST) ou “Unidades de Contexto Elementares” (UCE). Essa segmentação, geralmente em trechos de tamanho aproximado, não é um mero artifício técnico. Sua justificativa teórica reside na premissa de que o significado das palavras é construído localmente, em seu contexto imediato (Reinert, 1990). Ao analisar o vocabulário dentro desses pequenos segmentos, o método preserva as relações de coocorrência, em vez de tratar o documento como um simples “saco de palavras” descontextualizadas. Concomitantemente a essa etapa, o software realiza a lematização, um processo de redução das palavras à sua forma canônica ou radical, e isso garante que variações morfológicas de um mesmo conceito sejam tratadas como uma única entidade lexical, aumentando a consistência e a força da análise.
O núcleo do algoritmo opera através de um processo de partições dicotômicas (divisões em dois) sucessivas e hierárquicas (Reinert, 1990). O procedimento inicia com a totalidade do corpus, ou seja, todos os ST agrupados em uma única entidade. Em seguida, o algoritmo busca a divisão mais estatisticamente robusta deste conjunto, separando-o em dois subgrupos. O critério para essa divisão é maximizar a dissimilaridade lexical entre os dois novos subgrupos e, ao mesmo tempo, a similaridade lexical dentro de cada um deles. Este processo é então aplicado recursivamente a cada subgrupo recém-formado: o algoritmo seleciona um subgrupo e o divide novamente em dois, e assim por diante. Essa cascata descendente prossegue até que as classes atinjam um limiar de estabilidade ou um número mínimo de elementos, resultando em um conjunto final de classes estáveis e semanticamente coesas. O resultado é uma hierarquia na qual a primeira divisão representa a clivagem mais significativa do discurso, e as divisões subsequentes revelam distinções temáticas progressivamente mais finas. Essa abordagem, tecnicamente um tipo de algoritmo “ganancioso” (greedy algorithm), tem uma implicação metodológica importante: a estrutura final do dendrograma é dependente do caminho percorrido (Rakotomalala; Nouvel, 2007). A natureza da primeira e mais forte divisão condiciona todas as que se seguem. Isso significa que a classificação gerada não deve ser entendida como uma verdade ontológica sobre o texto, mas como o modelo hierárquico mais estatisticamente defensável que pode ser extraído a partir dos dados, dada a lógica de otimização do algoritmo.
Para cada possível divisão do corpus (ou de um subgrupo) em duas novas classes, o software constrói uma tabela de contingência. Essa tabela cruza a lista de palavras (formas ativas) com os dois potenciais novos grupos, registrando a frequência de cada palavra em cada grupo. O algoritmo então calcula o valor de \(\chi^2\) para essa tabela. Ele repete esse procedimento para muitas divisões possíveis e, finalmente, seleciona aquela que produz o maior valor de \(\chi^2\). Um valor elevado indica uma associação forte e estatisticamente significativa entre um conjunto de palavras e o primeiro grupo, e, por oposição, entre outro conjunto de palavras e o segundo grupo. Em essência, o qui-quadrado é o motor matemático que impulsiona todo o processo de classificação, garantindo que cada divisão seja a mais discriminante possível. O uso do \(\chi^2\) como critério de otimização significa que o método CHD está fundamentalmente orientado para a identificação de distintividade lexical. As classes que ele forma não são apenas agrupamentos de palavras que aparecem juntas, mas sim agrupamentos cujo vocabulário em uma classe é estatisticamente improvável de ocorrer na outra. Esse foco no contraste e na oposição é o que confere ao método sua notável capacidade de mapear os diferentes e, por vezes, concorrentes, “mundos” que compõem um discurso complexo como o jurídico.
A robustez da CHD não se baseia apenas na partição inicial, mas em um processo de refinamento que garante a qualidade e a estabilidade das classes finais. Após o algoritmo identificar a divisão ótima com base no maior valor de qui-quadrado, ele não a aceita de forma definitiva imediatamente. Em vez disso, inicia-se um passo de otimização iterativa. O algoritmo testa, um por um, cada ST de um grupo, movendo-o temporariamente para o grupo oposto e recalculando qui-quadrado global. Se essa realocação resultar em um aumento do valor, significando uma partição ainda mais coesa e distinta, o segmento é permanentemente movido. Esse processo de verificação e realocação é repetido várias vezes até que nenhuma outra mudança de segmento possa aumentar o valor do qui-quadrado. Somente nesse ponto a partição é considerada “estável” e “definitiva”. Esses mecanismos internos de controle de qualidade são cruciais, pois demonstram que o método não é uma “caixa-preta” que gera categorias arbitrárias. Pelo contrário, ele possui procedimentos incorporados para assegurar que os resultados sejam estatisticamente sólidos, replicáveis e fidedignos, conferindo validade e confiabilidade à análise.
A CHD, como aqui delineada, oferece vantagens para a análise do discurso jurídico: a capacidade de processar grandes volumes de texto de forma sistemática, o rigor estatístico que fundamenta a identificação de padrões, a descoberta de estruturas argumentativas latentes que poderiam passar despercebidas em uma leitura puramente qualitativa e a mitigação de certos vieses do pesquisador na fase de categorização inicial.
Contudo, é necessário reconhecer suas limitações. A qualidade da análise é intrinsecamente dependente da qualidade e da representatividade do corpus inicial. As decisões tomadas na preparação do texto, como a lematização ou a definição de palavras a serem ignoradas, podem influenciar os resultados. Mais fundamentalmente, a CHD é uma ferramenta de auxílio à interpretação, não uma máquina que produz a verdade sobre um texto.
O software não compreende semântica, ironia, polifonia ou a complexidade das teorias; ele detecta padrões de coocorrência lexical. A etapa de nomeação e interpretação das classes é um ato hermenêutico que depende inteiramente do pesquisador. Ao automatizar a tarefa de detecção de padrões, a CHD libera o pesquisador para se concentrar na tarefa de ordem superior que lhe é própria: a atribuição de significado. A adoção desta metodologia representa, em última análise, um compromisso com uma forma de pesquisa jurídica mais transparente, sistemática e empiricamente fundamentada, em uma profícua colaboração entre máquina e intérprete.